How To Draw And Paint For Profit
Drawing is an art of illusion—flat lines on a flat sheet of newspaper look like something real, something full of depth. To achieve this effect, artists utilize special tricks. In this tutorial I'll bear witness you these tricks, giving you the key to cartoon three dimensional objects. And we'll do this with the aid of this beautiful tiger salamander, as pictured past Jared Davidson on stockvault.
Why Sure Drawings Look 3D
The salamander in this photograph looks pretty three-dimensional, right? Let's turn it into lines now.

Hm, something's wrong hither. The lines are definitely right (I traced them, after all!), just the drawing itself looks pretty apartment. Certain, it lacks shading, but what if I told you that y'all can depict three-dimensionally without shading?
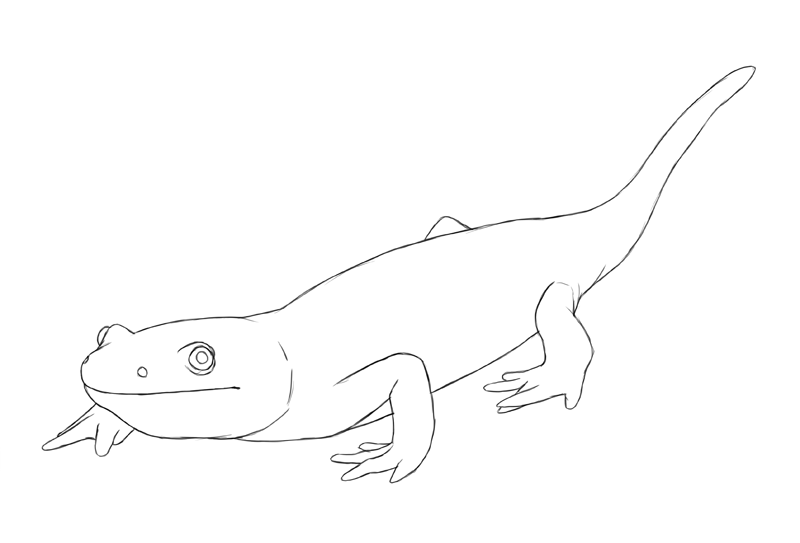
I've added a couple more lines and… magic happened! At present it looks very much 3D, maybe even more than the photo!
Although you don't see these lines in a terminal cartoon, they affect the shape of the design, skin folds, and even shading. They are the key to recognizing the 3D shape of something. So the question is: where do they come from and how to imagine them properly?
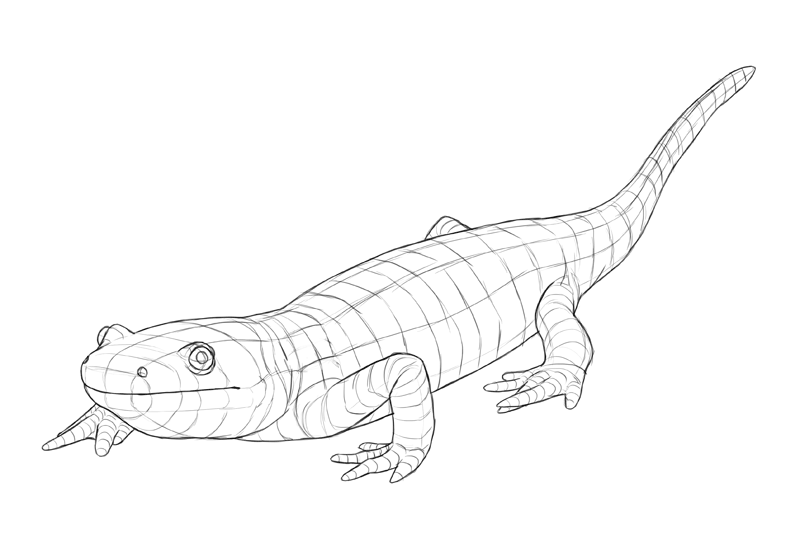
3D = 3 Sides
Every bit you remember from school, 3D solids have cantankerous-sections. Because our salamander is 3D, it has cross-sections as well. And so these lines are zippo less, naught more, than outlines of the torso'due south cross-sections. Here's the proof:

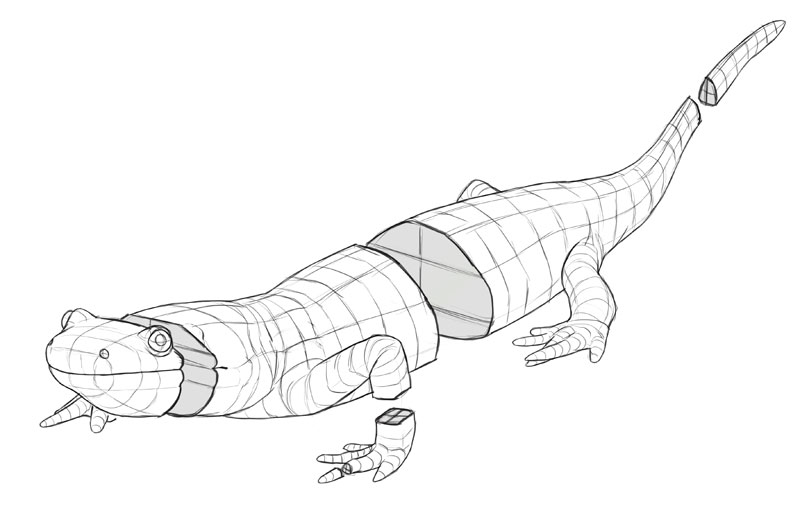
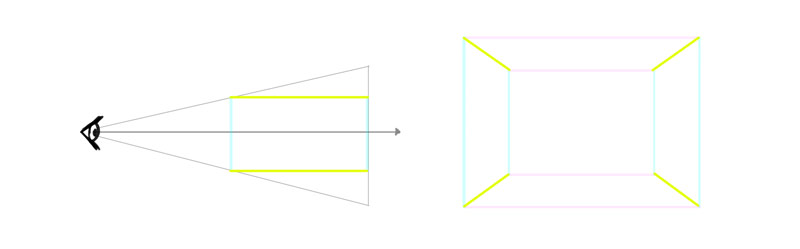
A 3D object can exist "cut" in 3 unlike means, creating 3 cantankerous-sections perpendicular to each other.
Each cantankerous-department is second—which means information technology has ii dimensions. Each 1 of these dimensions is shared with one of the other cross-sections. In other words, 2nd + second + 2D = 3D!
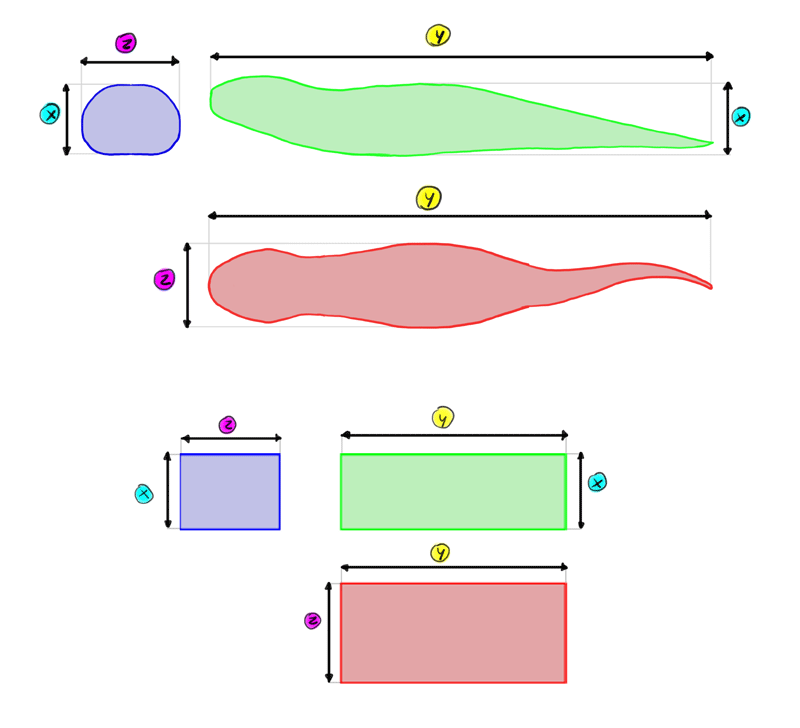
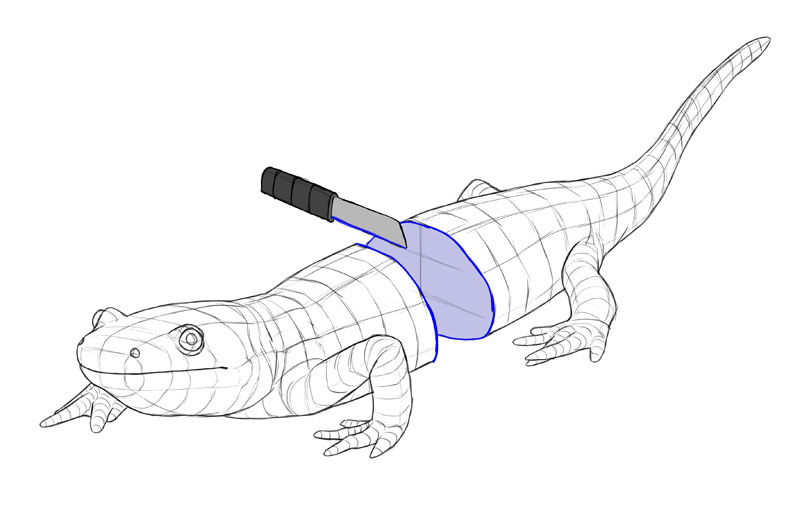
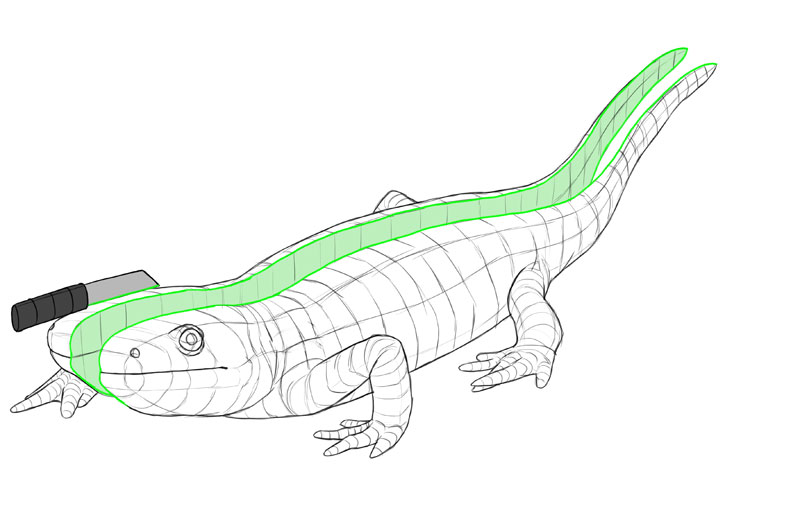
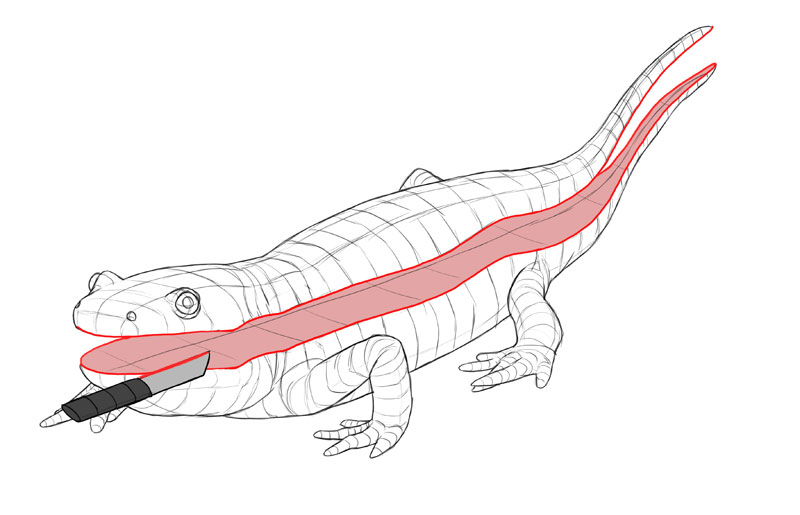
So, a 3D object has iii second cantankerous-sections. These 3 cantankerous-sections are basically iii views of the object—here the greenish 1 is a side view, the blue ane is the front/back view, and the crimson one is the pinnacle/bottom view.
Therefore, a cartoon looks 2D if you can only see one or 2 dimensions. To make it await 3D, you need to show all three dimensions at the same time.

To make it fifty-fifty simpler: an object looks 3D if you tin can see at least ii of its sides at the same time. Here you lot can see the acme, the side, and the front of the salamander, and thus information technology looks 3D.
Only expect, what's going on here?
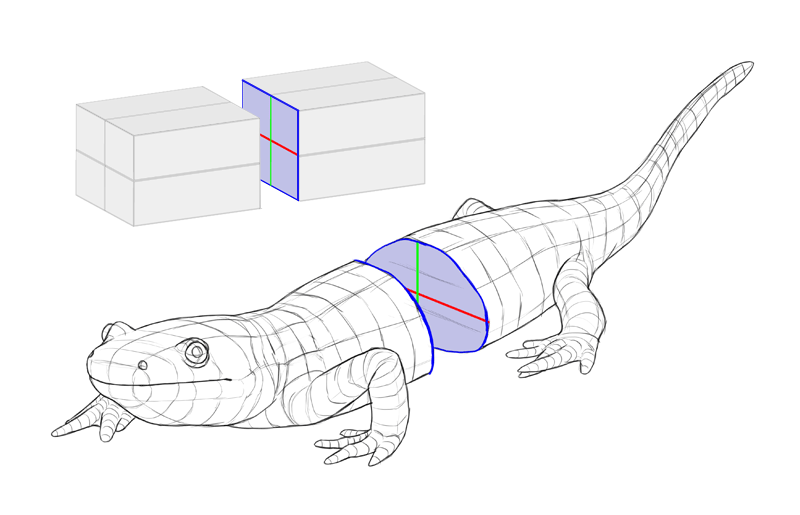
When you wait at a 2D cross-section, its dimensions are perpendicular to each other—there'south right angle between them. But when the same cross-section is seen in a 3D view, the angle changes—the dimension lines stretch the outline of the cantankerous-section.
Allow's practice a quick recap. A single cross-section is easy to imagine, only it looks flat, because it's 2D. To make an object wait 3D, y'all need to evidence at least two of its cross-sections. Simply when yous draw ii or more cross-sections at once, their shape changes.
This modify is not random. In fact, it is exactly what your brain analyzes to empathise the view. And so in that location are rules of this modify that your hidden mind already knows—and now I'm going to teach your conscious cocky what they are.
The Rules of Perspective
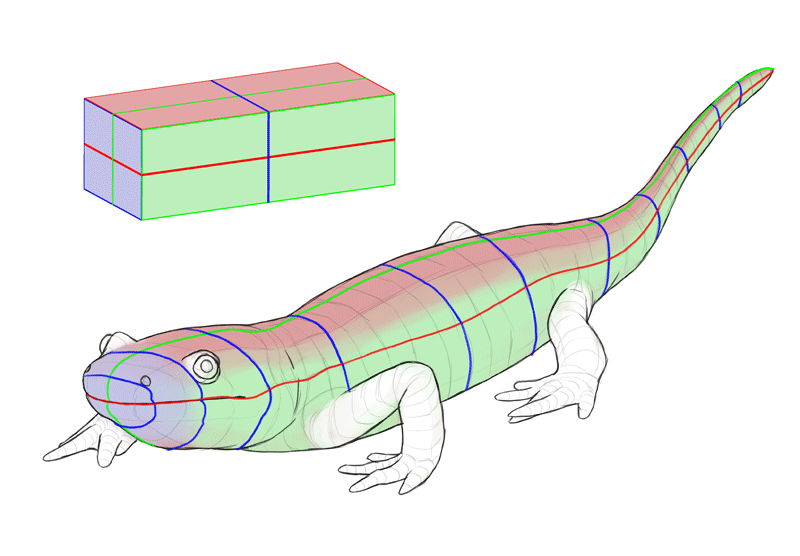
Here are a couple of dissimilar views of the aforementioned salamander. I take marked the outlines of all 3 cross-sections wherever they were visible. I've too marked the tiptop, side, and forepart. Take a good look at them. How does each view affect the shape of the cross-sections?
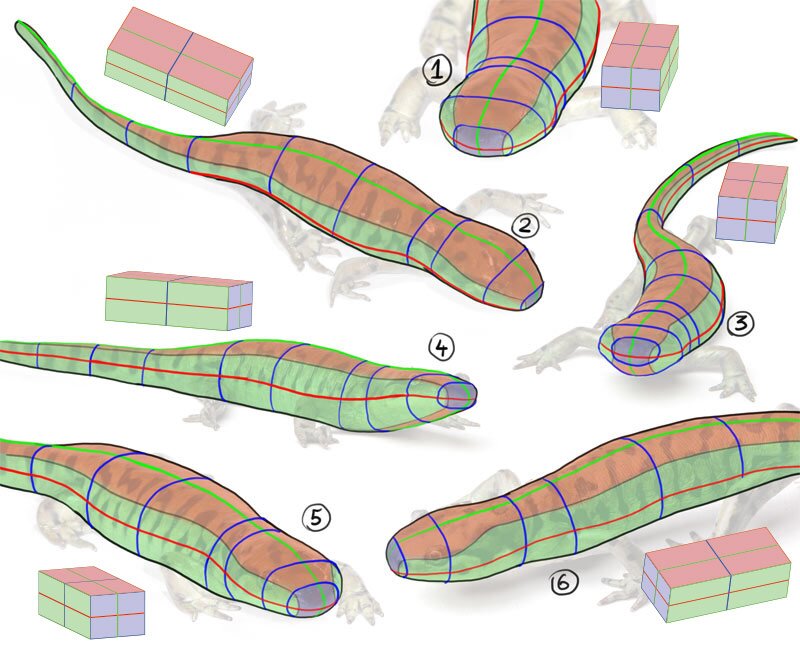
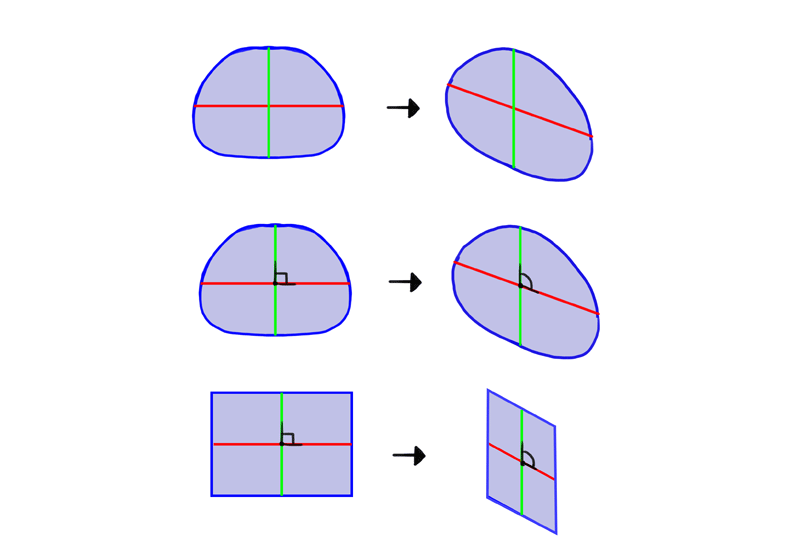
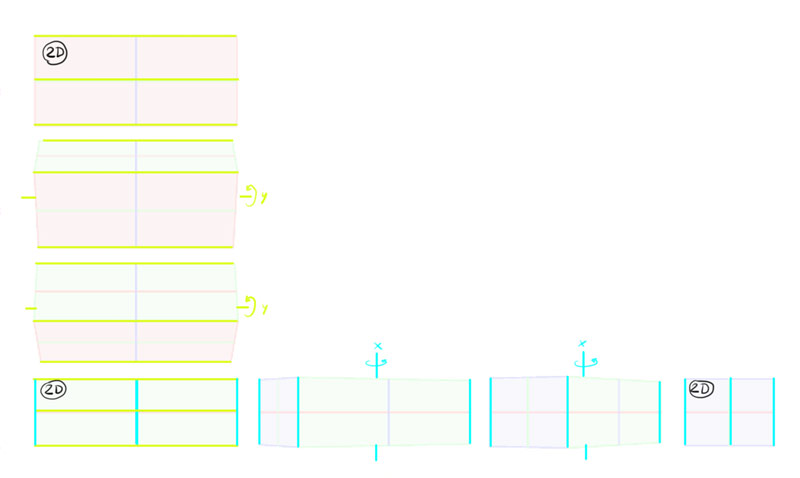
In a 2D view, yous have 2 dimensions at 100% of their length, and ane invisible dimension at 0% of its length. If you lot use one of the dimensions every bit an axis of rotation and rotate the object, the other visible dimension will give some of its length to the invisible one. If you continue rotating, one will go along losing, and the other will keep gaining, until finally the first one becomes invisible (0% length) and the other reaches its full length.
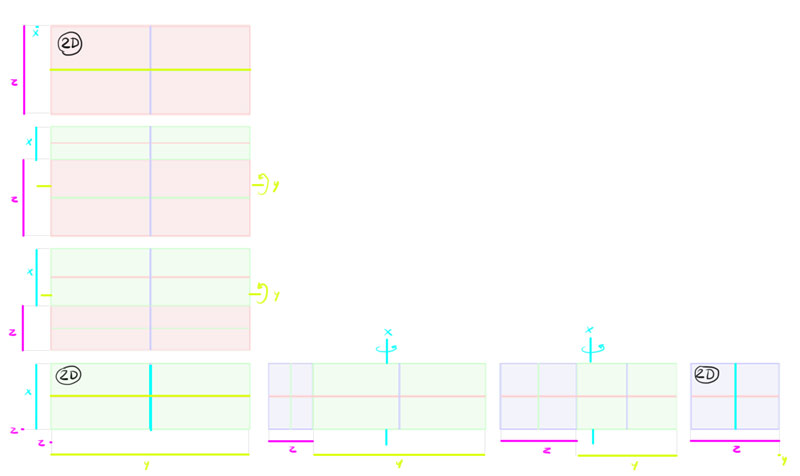
But… don't these 3D views await a little… apartment? That's right—there's one more thing that we need to accept into business relationship here. There'southward something chosen "cone of vision"—the further yous expect, the wider your field of vision is.
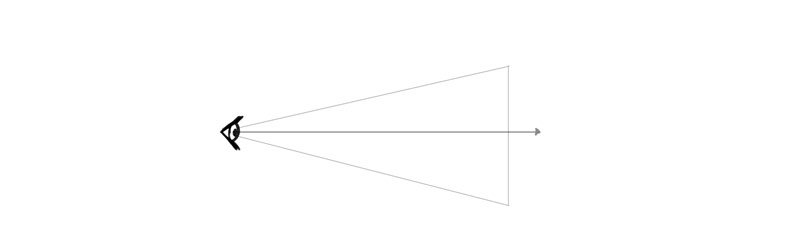
Because of this, you lot can comprehend the whole world with your hand if you identify information technology right in front end of your eyes, but it stops working like that when yous motility it "deeper" inside the cone (further from your eyes). This as well leads to a visual alter of size—the farther the object is, the smaller information technology looks (the less of your field of vision it covers).
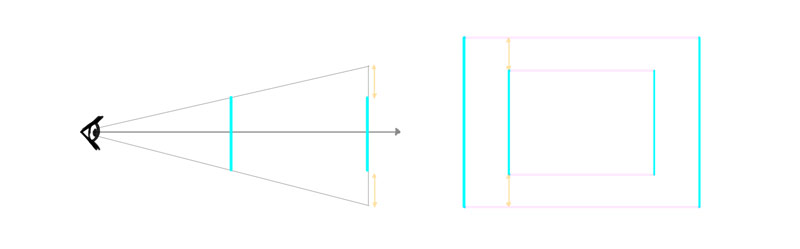
Now lets plow these two planes into two sides of a box by connecting them with the third dimension. Surprise—that tertiary dimension is no longer perpendicular to the others!
So this is how our diagram should actually await. The dimension that is the axis of rotation changes, in the cease—the edge that is closer to the viewer should exist longer than the others.
It'southward important to remember though that this effects is based on the distance between both sides of the object. If both sides are pretty shut to each other (relative to the viewer), this effect may be negligible. On the other hand, some camera lenses can exaggerate it.

Then, to describe a 3D view with ii sides visible, you identify these sides together…
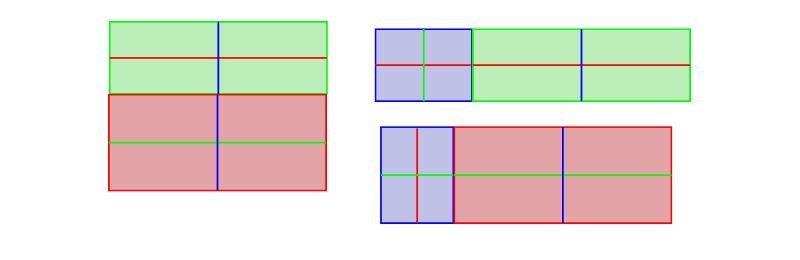
… resize them accordingly (the more than of one you want to show, the less of the other should be visible)…
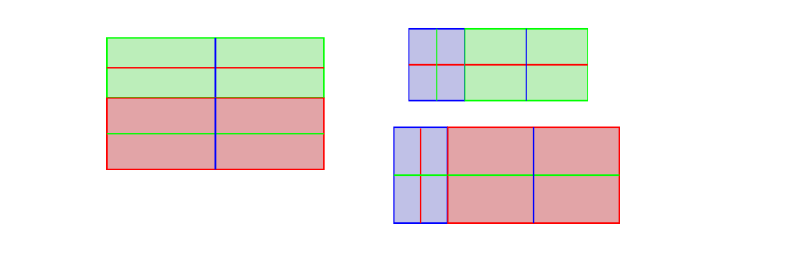
… and make the edges that are farther from the viewer than the others shorter.
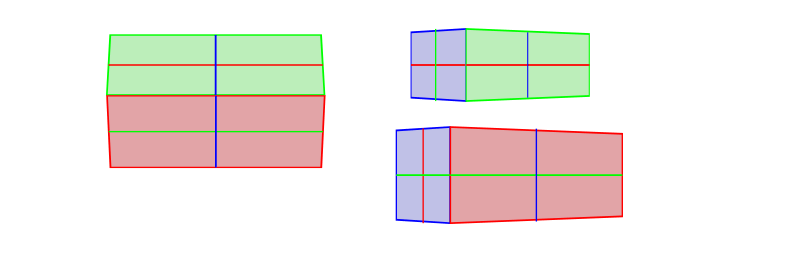
Here's how it looks in do:
But what about the third side? Information technology'south impossible to stick it to both edges of the other sides at the same time! Or is it?
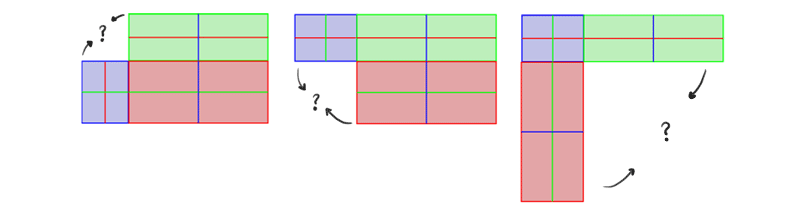
The solution is pretty straightforward: cease trying to keep all the angles correct at all costs. Slant one side, then the other, and and then make the third i parallel to them. Like shooting fish in a barrel!
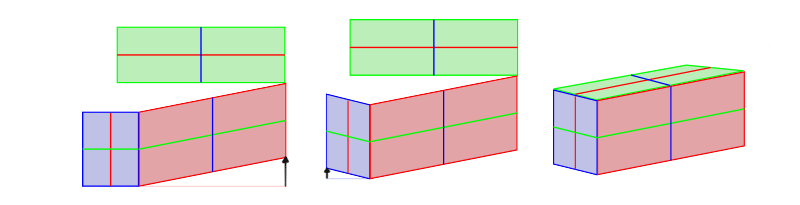
And, of course, let's not forget about making the more distant edges shorter. This isn't always necessary, but it'due south good to know how to do information technology:
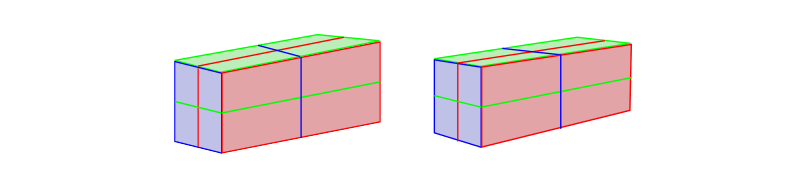
Ok, so you need to slant the sides, but how much? This is where I could pull out a whole prepare of diagrams explaining this mathematically, just the truth is, I don't practice math when drawing. My formula is: the more you lot camber ane side, the less you slant the other. Only wait at our salamanders again and bank check it for yourself!

But if you lot want to draw creatures like our salamander, their cross-sections don't really resemble a square. They're closer to a circumvolve. Only like a square turns into a rectangle when a 2d side is visible, a circumvolve turns into an ellipse. Simply that's non the end of it. When the third side is visible and the rectangle gets slanted, the ellipse must go slanted too!
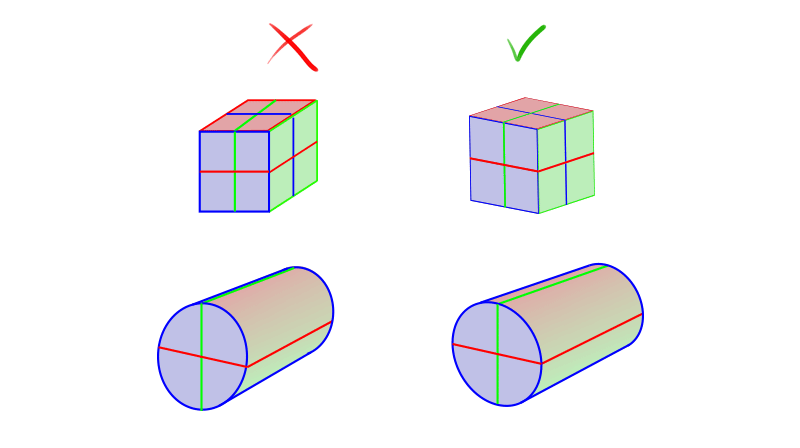
How to slant an ellipse? Just rotate it!
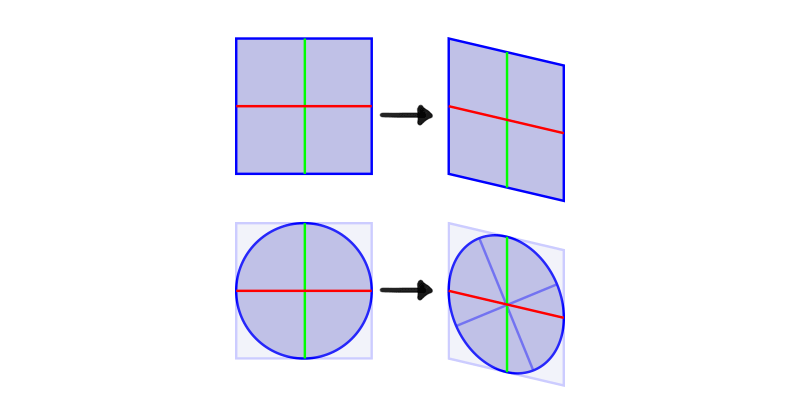
This diagram can assist you memorize it:
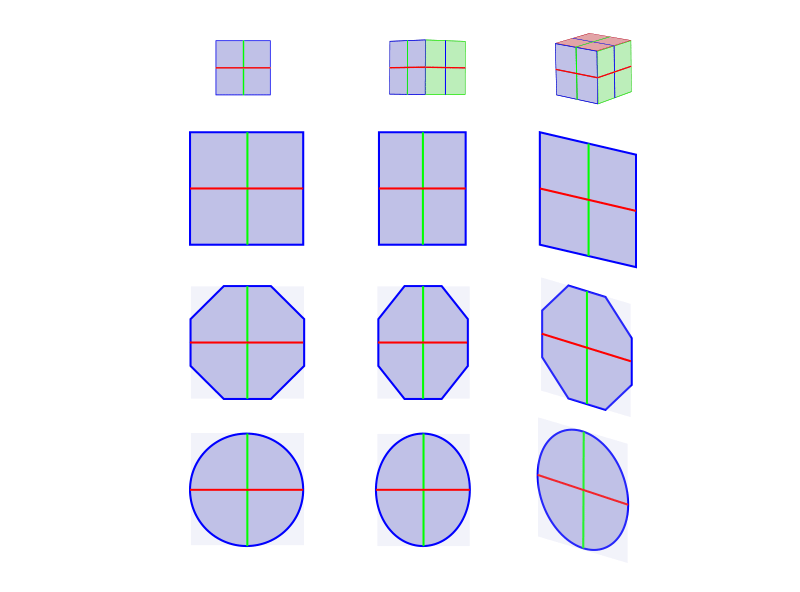
Multiple Objects
And so far we've only talked nigh drawing a single object. If you want to describe 2 or more objects in the same scene, there'south usually some kind of relation between them. To show this relation properly, decide which dimension is the axis of rotation—this dimension will stay parallel in both objects. Once you practise it, you tin do whatever yous want with the other two dimensions, as long equally yous follow the rules explained earlier.
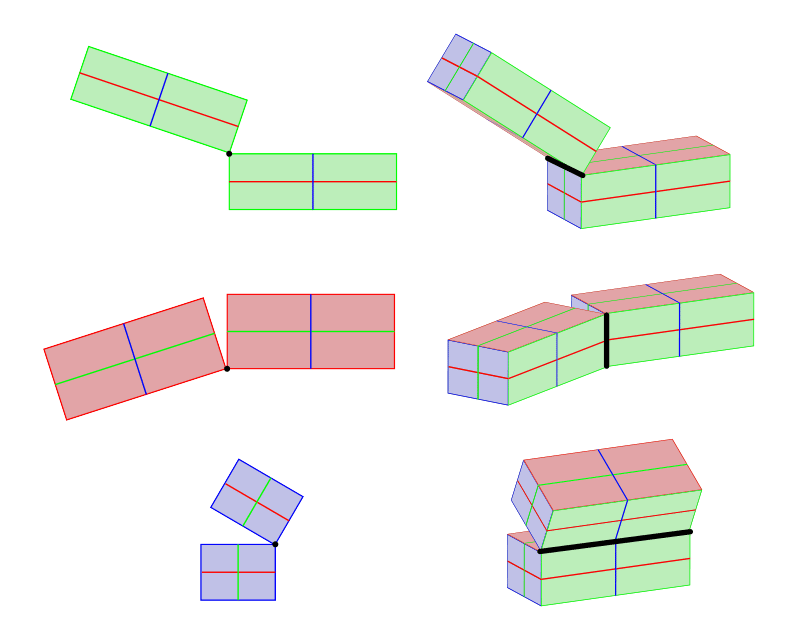
In other words, if something is parallel in ane view, and then it must stay parallel in the other. This is the easiest way to cheque if y'all got your perspective correct!

In that location'southward another type of relation, called symmetry. In second the axis of symmetry is a line, in 3D—it's a plane. Just it works but the same!
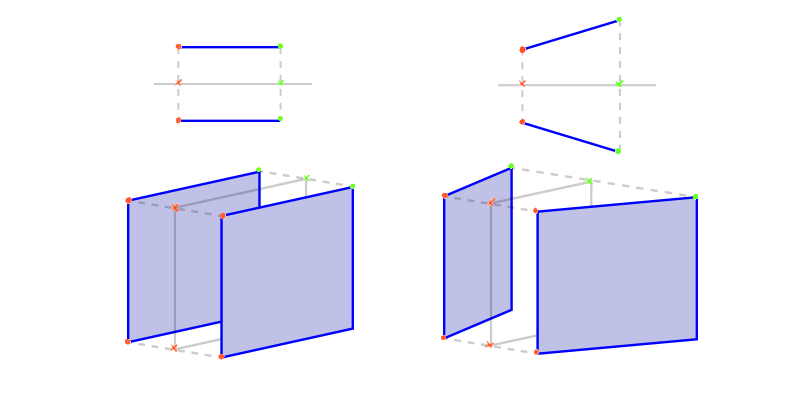
You don't demand to draw the plane of symmetry, simply you should be able to imagine it right between two symmetrical objects.
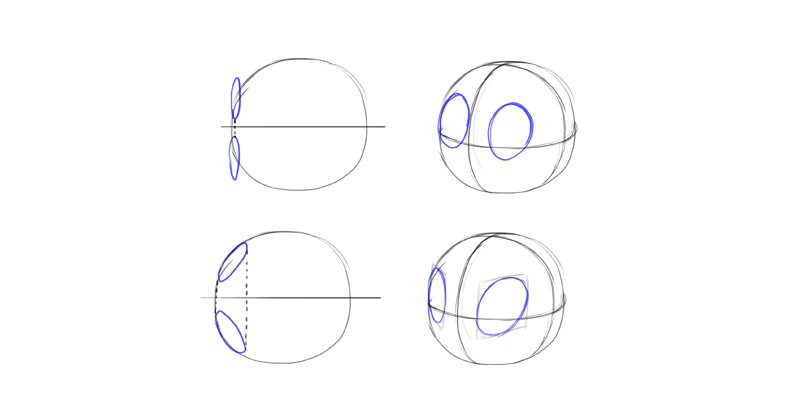
Symmetry will aid you with difficult cartoon, similar a head with open jaws. Here figure 1 shows the angle of jaws, figure 2 shows the axis of symmetry, and figure iii combines both.
3D Cartoon in Practice
Exercise i
To empathise it all better, you lot tin can try to notice the cantankerous-sections on your own now, cartoon them on photos of real objects. Offset, "cutting" the object horizontally and vertically into halves.


Now, find a pair of symmetrical elements in the object, and connect them with a line. This will be the third dimension.

Once you take this direction, y'all tin can draw it all over the object.

Keep drawing these lines, going all around the object—connecting the horizontal and vertical cantankerous-sections. The shape of these lines should be based on the shape of the third cross-section.

Once you're done with the big shapes, yous can practise on the smaller ones.

You'll before long observe that these lines are all yous demand to describe a 3D shape!
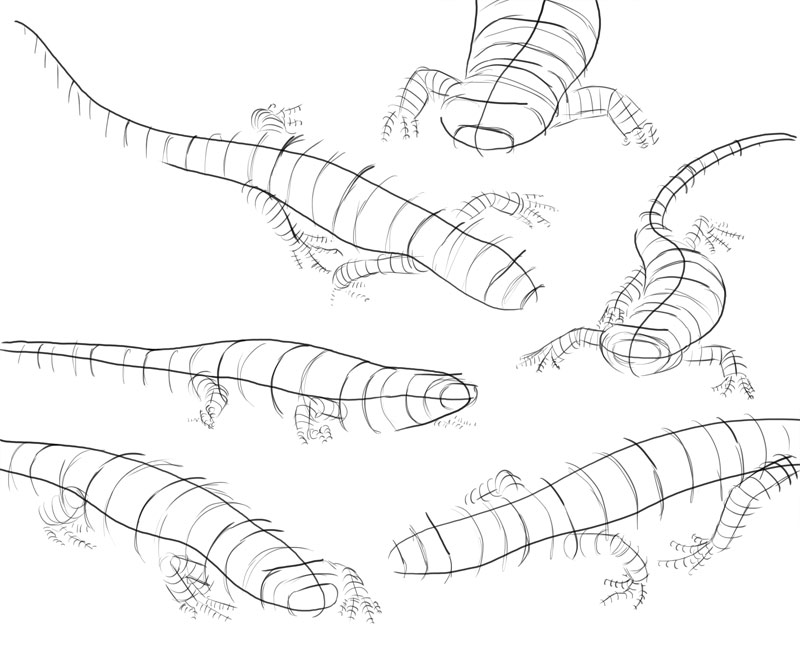
Exercise 2
You can do a like exercise with more complex shapes, to better understand how to draw them yourself. First, connect respective points from both sides of the body—everything that would be symmetrical in top view.

Marking the line of symmetry crossing the whole torso.

Finally, try to observe all the simple shapes that build the final grade of the body.
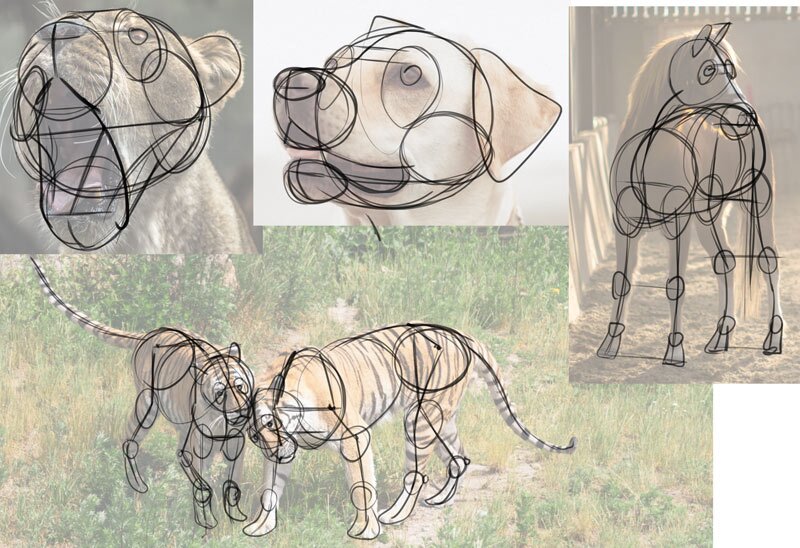
At present you have a perfect recipe for cartoon a similar animal on your ain, in 3D!
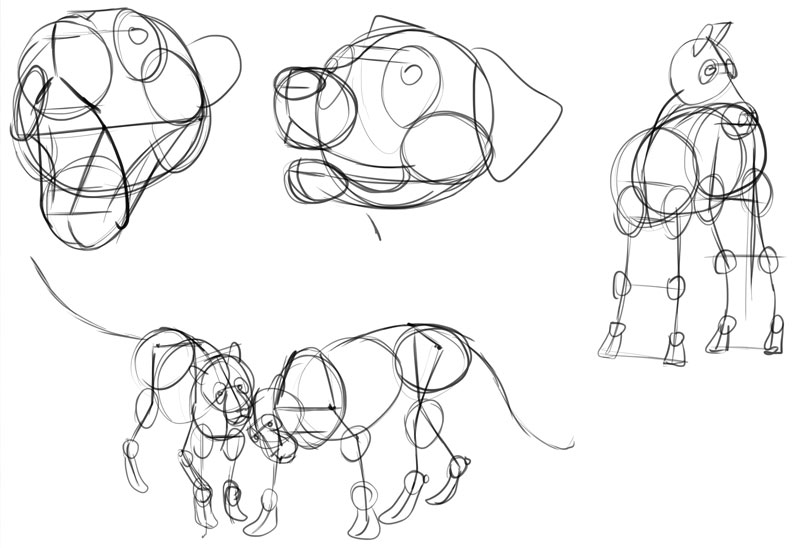
My Procedure
I gave you all the information you need to draw 3D objects from imagination. Now I'm going to prove yous my own thinking procedure behind drawing a 3D creature from scratch, using the knowledge I presented to y'all today.
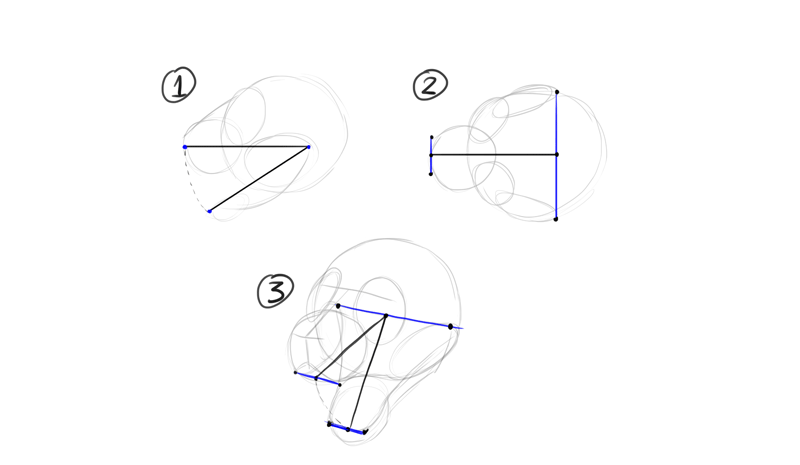
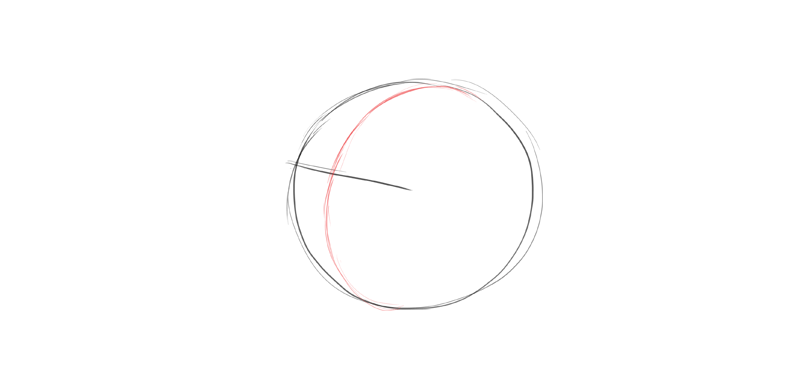
I ordinarily start cartoon an animal head with a circle. This circle should contain the cranium and the cheeks.

Adjacent, I depict the eye line. It'southward entirely my conclusion where I want to identify it and at what angle. But once I make this conclusion, everything else must be adjusted to this first line.
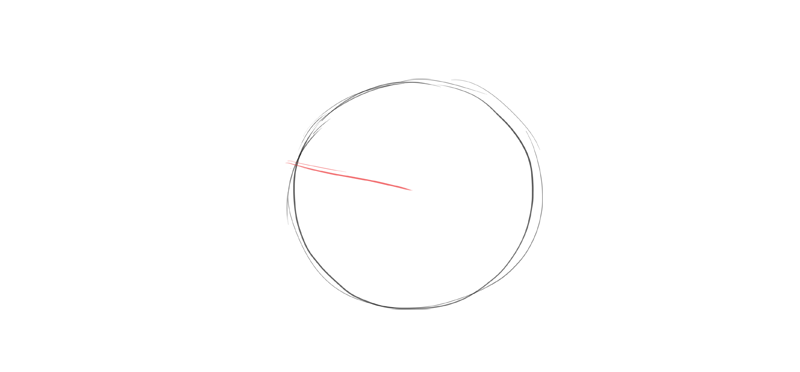
I draw the heart line between the eyes, to visually separate the sphere into ii sides. Tin you lot notice the shape of a rotated ellipse?
I add another sphere in the forepart. This will be the cage. I discover the proper location for information technology by drawing the nose at the aforementioned fourth dimension. The imaginary airplane of symmetry should cut the nose in half. Also, notice how the olfactory organ line stays parallel to the eye line.
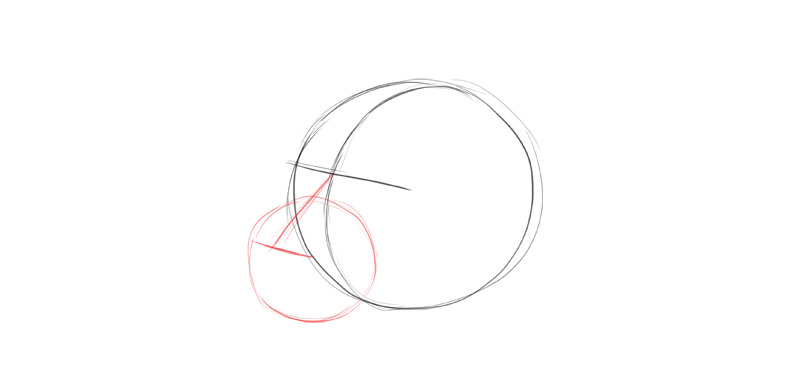
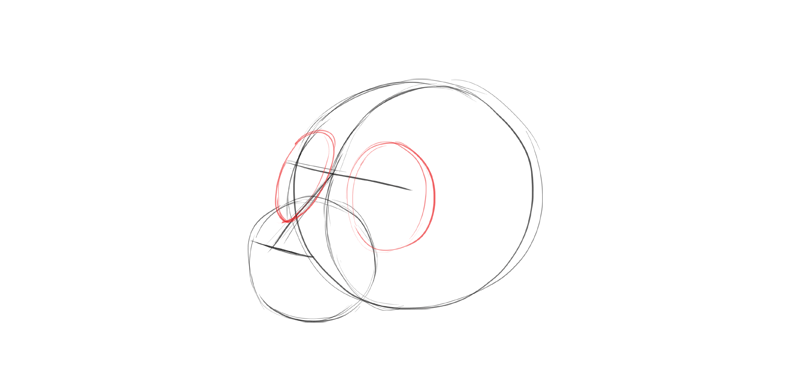
I draw the the expanse of the center that includes all the bones creating the heart socket. Such big area is easy to describe properly, and it will assist me add the eyes later on. Keep in heed that these aren't circles stuck to the front of the face—they follow the curve of the master sphere, and they're 3D themselves.
The mouth is so easy to describe at this betoken! I just have to follow the direction dictated by the centre line and the nose line.
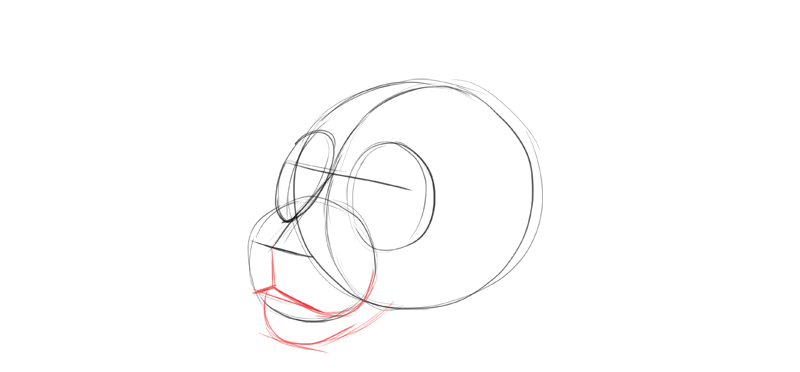
I draw the cheek and connect it with the chin creating the jawline. If I wanted to draw open jaws, I would draw both cheeks—the line between them would be the axis of rotation of the jaw.
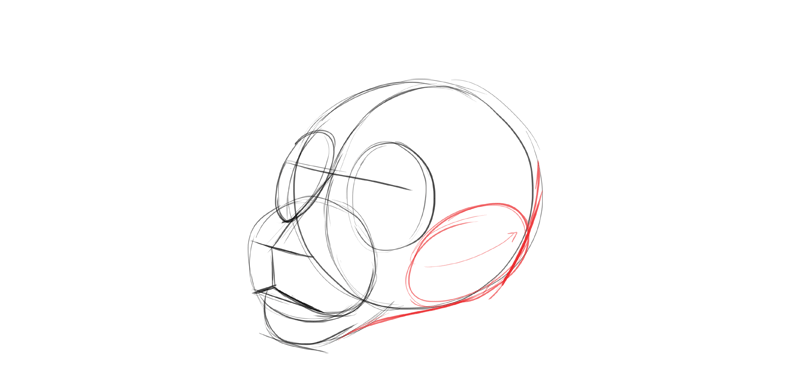
When cartoon the ears, I make sure to draw their base on the same level, a line parallel to the eye line, but the tips of the ears don't accept to follow this rule so strictly—it's because usually they're very mobile and tin can rotate in diverse axes.

At this point, adding the details is as easy every bit in a 2D drawing.

That's All!
It's the terminate of this tutorial, but the beginning of your learning! You should now be prepare to follow my How to Depict a Large True cat Head tutorial, as well as my other animal tutorials. To do perspective, I recommend animals with elementary shaped bodies, like:
- Birds
- Lizards
- Bears
You should also find information technology much easier to sympathize my tutorial about digital shading! And if you want even more than exercises focused directly on the topic of perspective, you'll like my older tutorial, full of both theory and exercise.
Source: https://monikazagrobelna.com/2019/11/25/drawing-101-how-to-draw-form-and-volume/
Posted by: stameypursee.blogspot.com


0 Response to "How To Draw And Paint For Profit"
Post a Comment